فرهنگ امروز/ ترجمه: علیرضا محمدی*:
فلسفهی ریاضی لاکاتوش منبعث از سه منبع عمده است:
۱- ابطالگرایی روششناسانهی پوپر که با جرح و تعدیل آن به ابطالگرایی پیچیده میرسد.
۲- استفاده از قواعد راهیابانهی پولیا که در آن ریاضیات فرمالیستی مورد نقد قرار میگیرد و در حقیقت ریاضی را از شکل صوری بهصورت یک فعالیت اجتماعی درمیآورد. کتاب برهانها و ابطالهای لاکاتوش به پیروی از شیوهی پولیا در راهیابی به ریاضی انتقادی نگارش شده است.
۳- دیالکتیک هگل که به تأسی از سهگانهی هگلی (تز، آنتیتز و سنتز) شیوهی رشد و توسعهی مفاهیم ریاضی را نیز مانند علوم دیگر میداند و شکوفایی آن را در چارچوب مطرح شدن آنتیتزهای مختلف در مقابل تز طرح شده و ایجاد سنتز و ترکیبات جدید میداند.
![]() گابورکوترواتز
گابورکوترواتز
ایمره لاکاتوش (۱۹۷۴-۱۹۲۲) بهوسیلهی حداقل دو گروه از فلاسفه مورد عنایت و توجه قرار گرفته است؛ برای فلاسفهی علم، او بزرگترین مدافع عقلانیت علمی به شمار میرود: او عقیدهی عقلانیت روششناسانهی آنی[۱] را رها کرد و آن را با روششناسی تاریخانگارانه جایگزین کرد که بر مبنای مفهوم «بازسازی عقلانی» بنا شده بود. برای فلاسفهی ریاضیات، او یک نقدکنندهی جدی برای مکتب صورتگرایی[۲] به شمار میرود و به جای انواع ریاضیات صوری آکسیوماتیک بر قاعدهی راهیابانه [۳] روندهای تاریخی ساختن تئوری و مفاهیم تأکید کرد. این دو مظهر اصلی کارهای لاکاتوش به ندرت در درون یک قالب فلسفی واحد مورد بحث قرار گرفتهاند و البته بدون دلیل نیست: لاکاتوش خودش هرگز تلاش نکرد که این دو زمینه را با هم هماهنگ کند، علایمی وجود دارد که نشان میدهند او قصد ساختن یک زمینهی مشترک برای آنها را داشت، ولی شاید پروژهی او قبل از مرگش دارای یک طرح مشخص نبود.
زمینهی فلسفهی ریاضیات لاکاتوش
لاکاتوش در بخش سپاسگزاری در رسالهی دکتریاش که در زمینهی فلسفهی ریاضیات بود ذکر میکند که بیشترین اثرات را در فلسفهی خودش از سه نویسنده گرفته است. این ذکر او بسیار جالب است و به ما کمک میکند که محرکها و اهداف او را بشناسیم. منابع و افرادی که او ذکر میکند به شرح زیر هستند:
تئوری ابطالگرایانهی پوپر؛ در پایان دههی ۱۹۵۰ و آغاز دههی ۱۹۶۰ وقتی او به طور عمده بر روی فلسفهی ریاضیات کار میکرد، تحت سیطره و تأثیر قوی کارل پوپر قرار داشت.[۴] و[۵] پوپر اصطلاح «ابطال» (Falsification) را برای رد کردن تئوریها بهوسیلهی واقعیات تجربی مورد استفاده قرار داد و تز عمدهی او آن بود که هیچ اثبات تجربی برای تئوریهای علمی وجود ندارد. لاکاتوش این تأکید بر مبنای ابطال را به شیوهای انجام داد که منحصراً بر مبنای برهانها قرار دارد و نشان داد که وقتی ریاضیدانان کار ریاضیاتی میکنند پس آنها عیناً تئوریهای دیگری را ابطال میکنند. این تأکید، تصویر ایدئال ما از ریاضیات (که در ریاضیات فقط با برهانها کار میکند) را به سمت فعالیت و کار ریاضی سوق میدهد.
راهیابانههای جورج پولیا؛ [۶] لاکاتوش هنگامی که هنوز در مجارستان بود و برای مؤسسهی ریاضی کار میکرد با ایدههای پولیا آشنا شد.[۷] پولیا بر روی نقش قواعد راهیابانه در تمرین واقعی ریاضیات تأکید کرد: توجه او بر روی ریاضیات غیرصوری بود و با این روش سروکار داشت که چگونه ریاضیدانان به نتایج خود میرسند. لاکاتوش نقطهنظر رسمی در فلسفهی ریاضیات را کنار گذاشت و این عقاید را در حمله به مکتب صورتگرایی به کار گرفت.
۳- دیالکتیک هگلی؛ تأثیر هگل بسیار زود خود را بر لاکاتوش در سالهای دانشگاه در مجارستان آشکار کرد، هنگامی که او درگیر فلسفه و ایدئولوژی لوکاچی مارکسیست بود.[۸] اما ردپای عقاید هگلی را میتوان در آخرین نوشتههای فلسفی او ملاحظه کرد و به خصوص در فلسفهی ریاضیات او حاضر است. در آموزش فلسفی، لاکاتوش فراگرفت که بحث از یک موضوع معین نمیتواند به مطالعه در قالب مفهومی ثابت یک سیستم صلب محدود شود، بلکه میباید به دیالکتیک مفهومی تبدیل شود که کمک به رشد و گسترش موضوع میکند و خودش را نشان میدهد؛ او یاد گرفت که تأکید بر روی پیشرفت است و بر روی حالات ایستا نیست؛ فلسفهی ریاضیات میباید یک فلسفهی پویا باشد نه فلسفهی قطعی ایستا و کمتر بر روی شناخت متکی باشد و بیشتر بر روی رشد و گسترش و شناخت.
انواع علوم قیاسی
به خاطر فهمیدن اینکه کجا ریاضیات در نقشهی روششناسی همهی علوم جاگذاری شده است، لاکاتوش یک طبقهبندی از علوم را ارائه میدهد؛ برای مثال سیستمهای آکسیوماتیک- قیاسی. میتوان بین دو گروه از انواع اساسی تفاوت و تمایز قائل شد، یا دو «قطب» از این سیستمها: سیستمهای اقلیدسی وجود دارد و از طرف دیگر سیستمهای شبهتجربی (نگاه کنید به طرح ۱)؛ آنچه در این نوع از سیستمها مشترک است «روح» قیاسی-آکسیوماتیک است؛ یعنی هر دو برخی جملات را بهعنوان پایه («اصول موضوعه») در نظر میگیرند و سعی میکنند بهوسیلهی قیاس منطقی بیشتر جملات («قضیهها») را از این اصولموضوعه استخراج کنند. تفاوت اصلی شیوه و روش در این سیستمها به نحوهی ارتباط آنها با «صدق» و «کذب» بستگی دارد.
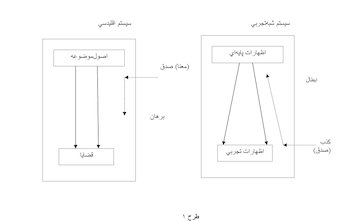
در مورد علوم اقلیدسی، صدق از «بالا» در سطح اصول موضوعه به سیستم «تزریق» شده است. در اینجا صدق از بالا به پایین به سمت قضایا بهصورت خودبهخود به ارث رسیده است، چون ماهیت سیستم قیاسی است که صدق مقدمات، صدق نتیجه را موجب میشود. این قطعیت که ارث غیرقابل ابطالی است و در طول مسیر قیاس جریان دارد، برهان (proof) نامیده میشود. اگر صدق اصلموضوعه به طریقی فرض شده است، صدق و اعتبار همهی سیستم نیز مفروض است. این ارزشِ آن است که راههای قیاس نه فقط «صدق نگهدارنده» هستند بلکه «معنا نگهدارنده» نیز هستند؛ بنابراین معنای این اصطلاحات در سطح اصولموضوعه وارد سیستم میشود (بهوسیلهی تعاریف) و در طول برهان به ارث میرسد.
در مورد سیستمهای شبهتجربی، این موقعیت کاملاً مخالف است: منبع صدق، قابل مقایسه با تجربه است (در معنای وسیع)، بنابراین این پایان کار است، «انتهای» جملات که فرد بتواند روشهای صدق را نشان دهد. ولی استنتاج قیاسی اینگونه است که صدق نمیتواند از پایین به بالا حفظ شود، چون نتیجه، فرد را قادر نمیکند تا تصمیمگیری کند که آیا مقدمات صادق هستند یا خیر (ممکن است بگوییم که استقرا یک رویهی اصولی در این طرح قیاسی نیست[۹]). از طرف دیگر کذب از پایین به بالا به ارث رسیده است، چون کذب نتیجهی مستلزم کذب (حداقل یکی از) مقدمات است؛ بنابراین سیستمهای شبهتجربی با ابطال کار میکنند. [۱۰] ما ذکر میکنیم که مفاهیم از «پایین به بالا» نمیتواند به ارث برسد و بنابراین در مورد علوم تجربی آزادی قابل ملاحظه دربارهی معنای اصطلاحات وجود دارد، برخلاف علوم اقلیدسی. این نکته برای ریاضیات ثابت خواهد شد که ضروری است، بعد از اینکه با تعجب فراگرفتیم که ریاضیات به این گروه تعلق دارد.
در بیشتر دوران تاریخ علم ریاضیات نه تنها بهعنوان یکی از علوم اقلیدسی مورد توجه قرار گرفت، بلکه بهعنوان نمونهی ازلی آنها بود، بهعنوان دژ عقلانیت از جایی که ما میتوانیم یورش نهایی خود را بر بخشهای غیرقطعی معرفت بشری وارد کنیم که هنوز در برابر قدرت استدلال محض (اقلیدسی) تاب میآورد. ولی در اینجا یک مشکل بزرگ معرفتشناسانه پیش میآید: به خاطر جایگاه ریاضیات بهعنوان پادشاهی همهی علوم اقلیدسی، ما مجبور هستیم تا رویکردی قابل اعتماد از مکانیسمی که اصولموضوعی صادق را میسازد ارائه دهیم. لاکاتوش به طور عمده دربارهی دو کاندیدای معرفتشناسی ریاضیات اقلیدسی بحث میکند: منطقگرایی[۱۱] و صورتگرایی[۱۲].
نقص معرفتشناسیهای اقلیدسی
مطابق با نظر فلاسفهی منطقگرا (در ابتدا گوتلب فرگه و برتراند راسل جوان)، دلیل و بینه برای اصولموضوعات ریاضیات از شهود منطقی به دست میآید، از طرف دیگر، اصولموضوعه منطقاً جملات صادق هستند (یا قضایای منطقی) و نفی آنها خود متناقض است. در این مورد ابطالپذیری اصولموضوعه بر مبنای همان مبانی اعتبار قیاس فرض شده است (قدرت منطق) و چون منطق برخی نسبتهای عمیق با اهمیت فکر کردن دارد، بنابراین ریاضیات بدون تردید صادق است.
ولی نقص برنامهی منطقگرایی بلافاصله پس از تولد آشکار شد (و ازقضا یکی از هواداران آن، این کار را کرد، یعنی راسل انگشت خود را بر روی درد بیدرمان -پارادکس راسل- در سیستم صوری فرگه نهاد)؛ «شهود منطقی» که آنها قصد داشتند اعتبار ریاضیات را از آن بیرون بکشند و طرح تئوریکی آن بهوسیلهی تئوری مجموعهی خام و اولیه فرض شده است، ناسازگار است، درحالیکه سازگاری میتواند بهوسیلهی جایگزین کردن تئوری مجموعهی خام با تئوری مجموعهی آکسیوماتیک حاصل شود، این طرح جدید صوری دور از ظهور هر شهود منطقی ابطالپذیر خواهد بود؛[۱۳] بنابراین برنامهی منطقگرایی بر باد خواهد بود. برنامهی بعدی کوشش در جهت تثبیت یک قالب اقلیدسی برای ریاضیات بهوسیلهی برنامهی صوری دیوید هیلبرت بود. اگر نقص برنامهای منطقگرا ناشی از ناسازگاری به ارث رسیده بود، وظیفهی اصلی تأمین سازگاری برای ریاضیات است؛ بنابراین فیلسوف صورتگرا تئوریهای ریاضی را با سیستمهای نحوی صوری محض شناسایی میکند که میباید دو شرط عمده را برآورده کند: (¡ ) حسابان میباید سازگار باشند[۱۴] و (¡¡) میباید با توجه به نفی کامل شود، یعنی فرد میباید قادر باشد هر قضیهی آوردهشده در آن را هم ثابت و هم ابطال کند (پیدا کردن صادق یا کاذب بهوسیلهی روشهای شهودی و کمتر صوری).
لاکاتوش زمان منسوخ شدن این برنامه را ۱۹۳۱ قرار میدهد، یعنی هنگامی که کورت گودل دو قضیهی ناتمامیت را اثبات کرد که معیار برنامهی صورتگرایی غیرقابل دفاع است: هیچ تئوری صوری وجود ندارد (که به قدر کافی برای اهداف ریاضی قوی باشد) که بهصورت نحوی کامل باشد؛ و هیچیک از این تئوریها نمیتوانند ناسازگاری خودشان را اثبات کنند (بنابراین هیچ تئوری ناسازگار قابل اثباتی وجود ندارد که سازگاری همهی تئوریهای دیگر را بتوان از آن بیرون کشید). لاکاتوش میپذیرد که این نقص هنوز بهوسیلهی اکثر ریاضیدانان تأیید نشده است و آنها سعی میکنند تا این بیماری را در فرامنطق، تئوری برهان و سایر زمینهها نشان دهند، ولی فرض میکند که هر کوششی از این نوع میتواند نشان داده شود تا محدودیتهای اصلی برنامههای هیلبرت را نشان دهد.[۱۵] شهودها دربارهی سازگاری و تمامیت ناکافی هستند تا فلسفهی ریاضی اقلیدسی را اثبات کنند. به جای بحث بیشتر و کوششهای کماهمیتتر، لاکاتوش نتیجهی تاریخمحوری را میگیرد (که منطقاً اکید و درست نیست، بلکه بهوسیلهی اندیشههای قبلی اثبات شده است) که ریاضیات یک علم اقلیدسی نیست. معنای این جملات آن است که از یک طرف، ریاضیات ابطالناپذیر نیست: ما قادر نبودیم مکانیسمی پیدا کنیم که صدق ضروری این اصلموضوعه را تضمین کند؛ و همچنین از طرف دیگر، ریاضیات به طور محض و خالص اثباتپذیر نیست: اصولموضوعه به تنهایی نمیتوانند اقتداری داشته باشند که متد برهان معتبر را بسازند. به علاوه ما اغلب در جستوجوی اصولموضوعهی مناسب هستیم تا اعتبار قضایای معین را که میخواهیم ثابت کنیم تضمین کنیم (اصلاح کردن یا ترک کردن جملات پایهای مخالف معرفتشناسی برهان است و باطل است). بالاخره ریاضیات نمیتواند به طور خالص صوری باشد، چون سیستمهای صوری نمیتوانند از توقعات پایهای که ما میخواهیم برای آنها مطرح کنیم پیروی کنند.
ازدواج بین فلسفه و تاریخ ریاضیات
بعد از این رویکرد تاریخی خلاصه میتوانیم ببینیم که در یک نگاه کلی چه تصویری از ریاضیات میتوان داشت و یا تصویر ایدئال ریاضی چگونه است و چگونه میتوان اوهام و تصورات را دور انداخت. فلسفهی ریاضیات مجبور است از توصیف ریاضیات آنگونه که هست شروع کند، برای این کار، فلسفه میباید با تاریخ ریاضیات ازدواج کند؛ میباید به حوادث واقعی نگاه شود و روشهای رشد و توسعه را بررسی کند و یا پیدا کند و روشی را که در نحوهی رشد و شکوفایی معرفت ریاضی توضیح داده میشود، بیابد.[۱۶] این عقیده بهوسیلهی تزهای مشهوری بیان شده است: «تاریخ ریاضیات بدون راهنمایی فلسفه نابینا است، درحالیکه فلسفهی ریاضیات به طور چشمگیری به پدیدهای که در تاریخ ریاضیات حضور دارد بستگی دارد و بدون آن تهی است.» [۱۷]
بخش دوم از جملهی بالا میتواند به راحتی بهوسیلهی آنچه ما دیدهایم تعیین شود: هر فلسفهای که تاریخ آن موضوع را مورد توجه قرار ندهد چیزی به دست نخواهد آورد، چون مکانیسم کاری موضوع مورد بحث را نخواهد فهمید.[۱۸] اما اولین بخش از این تزها بیشترین مشکل را داراست، چون تعداد زیادی از مورخین نیستند که میپذیرند تحقیق تاریخی نمیتواند بدون استفاده از یک قالب فلسفی پیشرفت کند. ولی لاکاتوش وجود فلسفههایی را که مبتنی بر تاریخ نباشد تأیید نمیکند؛ مطابق با نظر او وقتی مورخین، علم به حوادث تاریخی واقعی رد میکنند، یک پیشمفهومی [۱۹] از آنچه ماهیت رشتهی علمی فرض است را دارند. مجموعهی اطلاعات تاریخ بسیار بزرگ و فراوان است و کنترل کردن همهی آنها باعث سردرگمی میشود و همچنین نمیتوان با هیچ سیستم درونی و یا روش خاصی آنها را در سیطره درآورد، بنابراین ما احتیاج داریم که پیشفرضهای قطعی و سویهدار را در اختیار داشته باشیم: مورخین به طور اجتنابناپذیری یک بازسازی عقلانی از تاریخ واقعی را ارائه میدهند. با توجه به این، در عوض سعی کردن برای خلاص شدن از شر پیشمفهومها (که غیرممکن است) میباید بهصورت آگاهانه بر روی این نقطه متمرکز شویم و با کمک تحقیق تاریخی به این سؤال جواب دهیم: «علم چیست؟[۲۰]»
اگر فلسفه بهصورت اجتنابناپذیری در تاریخ علم حضور دارد، پس ما باید از آن استفاده کینم.[۲۱] آنچه در ابتدا میفهمیم، نگاه به تاریخ ریاضیات بعد از تحلیل نقض مکتب صورتگرایی است، آن است که تئوریهای ریاضی بهصورت حساب صوری ارائه شده است. در عوض، حساب صوری بهوسیلهی ریاضیدانان ساخته شده است به این جهت که تئوریهای غیرصوری را دقیقاً بهصورت مفهومی درآوریم. همیشه یک تئوری غیرصوری قبل از سیستم صوری وجود دارد و ماهیت این تئوری مبهم توسط ثابت کردن قالب صوری منظم و مرتب شده است. به علاوه، این روند صورتبندی مکانیسم اکتشاف ریاضی است: رشد معرفت ریاضی بهوسیلهی ساختن رویکردهای صوری از شهود غیرصوری حاصل شده است؛ مجدداً با توجه به معرفتشناسی صدق تئوریهای ریاضی به صدق این تئوریهای غیرضروری منوط شده است، ولی این سؤال دوم بهوسیلهی لاکاتوش با یک شیوهی سنتی یگانه و منحصربهفرد پاسخ داده نشده است. انتزاع از تجربه؛ نظریهی روشنگرانهی قلمرو هویات افلاطونی درونی؛ با شهود ارائهشده توسط ساختن مفهومی اشیا، همهی این رویکردها میتوانند (با قدرت تغییر از موردی به مورد دیگر) مورد استفاده قرار گیرند، وقتی صدق را به تئوری غیرصوری در دسترس نسبت میدهیم؛ ولی فلسفهی ریاضیات با این بحث مورد توجه قرار نگرفته است، بلکه با شیوهای که در آن، این سیستم و مفاهیم صوری تثبیت شده است و با روندی که از حدسها به معرفت ختم میشود مورد بحث و توجه قرار گرفته است؛ این فلسفه، معرفتشناسی نیست بلکه روششناسی یا علم راهیابانه است.
روش برهانها و ابطالها
مهمترین نوشتههای لاکاتوش در فلسفهی ریاضیات برهانها و ابطالها است، یعنی یکسری از مقالات (که بعدها بهعنوان یک کتاب منتشر شد) که او از دومین رسالهی دکتریاش بهعنوان مقالاتی در زمینهی منطق اکتشاف ریاضی استخراج کرده بود (بخش عمدهی این کار «بازسازی عقلانی» از روندی تاریخی است که مطابق نظر نویسنده به طور فوقالعادهای برای روشن کردن رشد معرفت ریاضی مناسب است. این مطالعه، رشد مفهوم چندوجهیها را در طول قرون ۱۸ تا ۲۰ نشان میدهد. «تاریخ درونی» یا بازسازی عقلانی با «تاریخ بیرونی» تکمیل شده است -مجموعهای از حوادث تاریخی واقعی-). مراحل اصلی روند عمومی بهصورت زیر است (نگاه کنید به طرح ۲)
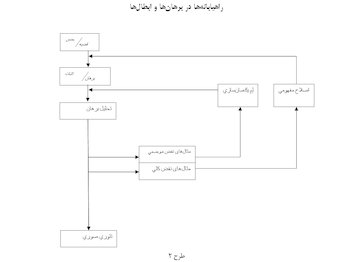
حدس خام: تحقیق ریاضی همیشه از یک مسئله شروع میشود (و میباید توجه کرد که همیشه به یک مشکل نیز ختم میشود).
این مشکل و مسئلهی شناخت شهودی نظم و یا ارتباطی است که نمیتوان آن را درون متغیرهای صوری تعریفشدهی تئوریهای موجود بیان کرد؛ بنابراین، بیان حدس خام مستلزم امکان برهان نیست: ما نیازمند یک تئوری صوری هستیم که در آن جملات میتوانند بهصورت یک قضیهی ثابت درآیند (منابع این «شناخت» میتوانند متنوع و محتمل باشند و آنها برای فلسفهی ریاضیات جالب نیستند، همانطور که ملاحظه کردیم وقتی ما از معرفتشناسی چشمپوشی میکنیم). در مورد آزمایششده، این انتظام تشخیص دادهشده حدس دکارتی-اقلیدسی است، برای مثال برای هر چندوجهی، تعداد رئوس به علاوه تعداد وجوه منهای تعداد یالها برابر دو میشود.
«خام» برای جملهی خود ارائه میکنیم، یک اثبات «شهودی» از اعتبار عمومی آن. در مورد بحث با این اثبات استدلالکوشی[۲۲] است: فهمیدن چندوجهی بهصورت ورقههای لاستیکی، اگر ما فرض کنیم که آنها را در طول یکی از یالها قطع میکنیم و بهصورت یکنواخت گسترش میدهیم، میتوانیم «ببینیم» که این جملات صادق است، ولی اجتماع ریاضیدانان به آشفتگی مفهوم «ورقههای لاستیکی» چندضلعی روی خودش نشان نخواهند داد و آنها به راحتی با مثالهای نقض سعی در نقض کردن آن خواهند داشت: مواردی که برای آنها حدس تأثیری ندارد. اکنون همهی انتقادات و نقض انتقادات حیاتی هستند، آنها موتورهای تطور تئوریها هستند.[۲۳]
مثالهای نقض میتوانند به دو بخش عمده تقسیم شوند: موضعی[۲۴] و کلی[۲۵]. مثالهای نقض موضعی آنهایی هستند که قضیهی ما را بهصورت کلی ابطال نمیکنند، آنها فقط «لمهای پنهان» را ابطال میکنند که ما ناآگاهانه خود را در صورت قضیهی خود محصور کردهایم؛ در این حالت ما «لمهای خطا» را با دیگری جایگزین میکنیم که با این کار اعتبار مثال نقض را بیرون میاندازیم. از طرف دیگر مثالهای نقض کلی آنهایی هستند که قضیهی ابتدایی ما را ابطال میکنند. اما، ما قضیهی خود و برهان آن را دور نینداختهایم، ولی ما مفاهیم و معانی درگیر را اصلاح میکنیم یا آن را دربارهی جملات مورد نظر دقیقتر بیان کنیم (برای مثال، چندضلعیها چه هستند).
در این روش، از طریق کنش و واکنش دیالکتیک برهانها، ابطال و تحلیل برهان، یک سیستم صوری از مفاهیم بهصورت تدریجی آفریده میشود و این طرحی از یک تئوری ریاضی جدید خواهد بود.[۲۶]
۳. تئوری قیاسی؛ بالاخره «برنامه تحقیقی» در تئوری صوری جدید پایان مییابد. همهی معانی اصطلاحات درون سیستم آکسیوماتیک ثابت شدهاند و بسیاری از تئوریها (که احتمالاً شامل تئوری اصلی نیز میشود) میتوانند از آن به دست آیند (در مورد مطالعاتی ما، تئوری جدید سیستم آکسیوماتیک است و توپولوژی جبر است. نگاه کنید به برهان و ابطالها).
در آخرین مرحله، فعالیت ریاضی به «حل کردن» معما[۲۷] تبدیل میشود (که قضیهها میتوانند در این تئوری ثابت شوند) و هیچ برنامهی مهیجی سر برنخواهد آورد. برای فلسفهی ریاضیات صورتگرایی -فقط این مرحله جالب است- شکل واقعی فعالیت ریاضی و برای لاکاتوش این خستهکنندهترین و کمجاذبهترین بخش است. مطابق نظر لاکاتوش، طرح رشد و توسعه میتواند در مورد ریاضیات یونان باستان نشان داده شود، یعنی تطور هندسه از تالس تا اقلیدس؛ [۲۸] جالبتر اینکه، لاکاتوش برای اعتبار این طرح در مورد تولد فیزیک مدرن نیز استدلال میکند: از «حدس خام» کپلر (که قابل اثبات درون هر تئوری فیزیکی موجود در زمان شناخت آنها نبود) تا پایهی اکسیوماتیک مکانیک نیوتنی. همانطور که در مقدمه ذکر کردیم برخی علایم وجود دارند، یعنی لاکاتوش در سال آخر زندگیاش فرقی بین علوم طبیعی و ریاضیات نمیدید، نه در روششناسی و نه در موضوع، بلکه متأسفانه برای فرمولبندی سادهی این نظریات، وقت کافی قبل از مرگش نداشت.
ما مجبور هستیم ذکر کنیم که این مثال نشان دادهشده در برهانها و ابطالها بیشتر در آن تئوریهای صوری جدید که متولد شدهاند را روشن میکند. این مثال ماهیت رشد ریاضی را نشان میدهد: چگونه فعالیت تحلیلی برهان در به دست آوردن موضوع حقیقی کمک میکند. ریاضیات بر اساس برهان بنا شده است، وقتی زمینهای از تحقیقات مورد علاقه به پایان آن میرسد، مرحلهی آکسیوماتیک، بسیار مورد توجه مکتب صورتگرا است؛ ولی بااینهمه این زمینه مرده و پوچ است. معرفی دامنهی تاریخی ریاضیات هدف فهم ریاضیات را بهعنوان یک پیشرفت حفظ میکند: در فلسفه آنچه برای ما مورد علاقه هست طرحهای صوری معرفت نیست بلکه رشد معرفت است؛ همانگونه که لاکاتوش تأکید میکند: در ریاضیات همهی رشد در رشد محتوا ایجاد شده است؛[۲۹] یعنی هر انتقادی که دقت روششناسی و اصطلاحشناسی را در زمینهی مورد بحث افزایش میدهد، میزان شناخت ما و فهم قابل دسترس برای روشهای علمی (برای مثال قیاسی) را افزایش میدهد.
نتیجه
احتمالاً به نظر میرسد که بینشهای عمیق و اصلی در فلسفهی لاکاتوش ناشی از آموزش متنوع و گوناگون لاکاتوش بوده باشد: از فلسفهی هگل لوکاچی به شیوهی تحلیلی صوری استدلال کمبریج رسیدن باعث تأثیرات متنوعی در زندگی آکادمیک او شد. این نظرات کاملاً متناقض، موجب تولید ایدههای مؤخر و پویا در فلسفهی او شد، بهطوریکه او هرگز شأن برای وضوح بخشیدن و یقین کردن یک سیستم فلسفی کامل و پایانی پیدا نکرد؛ چیزی که او بهعنوان امر غیرجالب توجه در مورد تئوریهای ریاضیات کنار میگذاشت. بیشترین چیزی که از او یادگار گذاشته شده است، عبارت است از: تأکید بر روی دامنهی تاریخی؛ اختصاص دادن به مسئلهی رشد و توسعه و کوشش برای فهم ریاضیات نه بهعنوان یک چیز صوری که غریبه با ما است، بلکه بهعنوان چیزی که توسط ریاضیدانان به کار گرفته میشود. او ریاضیات را از اسطورهی کامل بودن به قلمرو هستیهای بشری آورد که برای رسیدن به درجهی بالاتری از کامل شدن مسئولیت دارد که این رویکرد یک انقلاب کپرنیکی در فلسفهی ریاضیات است.
* این مقاله ترجمهی Imre laktos`s philosophy of Mathematics است که توسط Gabor Kutrovotz نوشته شده است. او استاد دانشگاه Eotvos Lorand بوداپست است.
۱-instant
۲-Formalism
[۳]- heuristic
۴- به فاصلهی نهچندان طولانیتر، او تئوری خودش در فلسفهی علم را بهعنوان رشد و تعمیم فلسفهی پوپر صورتبندی کرد.
۵-حداقل دو عنوان از نوشتههای ریاضی او به کارهای پوپر بازمیگردد: منطق اکتشاف ریاضیاتی هموزن و آهنگ با کتاب معروف پوپر با عنوان منطق اکتشاف علمی است ، درحالیکه برهانها و ابطالها با حدسها و ابطالهای پوپر همساز است.
[۶]- George Polya
۷- او حتی کتاب «چگونه آن را حل کنم» پولیا را به مجاری ترجمه کرد.
۸- به نظر میرسد که او در ابتدا با عقاید هگل آشنایی نداشت ولی بعد با این عقاید از طریق تفسیر لوکاچی در کتاب تاریخ و آگاهی طبقاتی آشنا شده بود.
۹- لاکاتوش منطق احتمالات را بهعنوان استثنا قرار میدهد، ولی او این مورد را اینگونه طرد میکند که جهت معرفت و شناخت ایجادشده بهوسیلهی علم، «حقایق» امکانی نمیتوانند بهعنوان یک راهحل اقناعی در نظر گرفته شوند.
۱۰- به بخش قبلی دربارهی نفوذ و اثر پوپر لاکاتوش با دلبستگی او به ابطالها بنگرید.
[۱۱]- Logicisim
[۱۲]- Formalism
۱۳- برخی اصولموضوعههای تئوری مجموعه تسرملو – فرانکل (یا اصولموضوعهی دیگری از تئوری مجموعه) از اینکه به طور آشکار صادق باشند دور هستند و اعتبار آنها (مانند در مورد اصلموضوع انتخاب) برای دههها در نیمهی اول قرن مورد بحث قرار گرفته بود.
۱۴- فرد میتوانست بگوید که سازگاری نیازمندی به صدق را ایجاب می کند؛ بنابراین برنامهی صورتگرا یک معرفتشناس اقلیدسی محض برای ریاضیات نیست، بلکه آن به این معنا است که مفهوم روششناسانهی اصلی آن برهان است.
[۱۵] یک مثال برهان سازگاری نوع گ؟؟ برای ریاضیات است که بر مبنای استقرای تراپایانی بنا شده است.
۱۶- به تأثیر هگل بر روی افکار لاکاتوش توجه کنید.
۱۷- این عبارت ایمانوئل کانت دربارهی رابطهی بین شهود و عقل است. لاکاتوش همین نظر را برای علم به کار برد (و از ریاضیات نیست) و او این جمله را در ابتدای یکی از مهمترین مقالاتش با عنوان «تاریخ و بازسازی عقلانی آن» قرار داده است.
۱۸- درهمان سالها که لاکاتوش نظریهی خود را اعلام کرد، یک ادعای مشابه بهوسیلهی توماس کوهن شکل گرفت که یک مورخ علم بود وامروزه به سختی هر فیلسوفی اعتبار این استلزام را در نظر داشته باشد.
[۱۹]- Preconception
۲۰- یا حتی : «عقلانیت علمی» چیست؟
۲۱- مفهوم «بازسازی عقلانی» بحثهای جالبی را باعث می شود و حتی امروزه در میان مورخین باعث دردسر و مزاحمت شده است. بحث عمومی از این مفهوم ما را به خارج از زمینهی تاریخ ریاضیات راهنمون خواهد شد و نیازمند یک تحلیل جزیی از فلسفهی علم لاکاتوش خواهد بود.
[۲۲]- Cauchy
۲۳- نقش انتقادات بهوسیلهی کارل پوپر که برای رویکرد عقلانی لازم است مورد تأکید قرار گرفته است. برای لاکاتوش ،که وجود روش علمی ثابتشدهی عقلانیت را نمیپذیرد ، این نقش از انتقادات و رویکرد عقلانی حتی بیشتر ضروری است.
[۲۴]- Local
[۲۵]- global
۲۶- در هنگام تطور «برنامهی تحقیقی»، «هستهی سخت» تعیین و مشخص شده است و «راهیابانهی مثبت» از برنامهی مورد نظر فعال است. نگاه کنید به اصطلاح شناسی فلسفهی علم که او برای فلسفه ی ریاضیات نیز به کار برده است.
[۲۷]- Puzzle Solving
۳۰- او به معلم و دوست سابقش یعنی Arpadszabo ارجاع میدهد که بهعنوان یک مورخ خوب ریاضیات شناخته شده است.
۲۹- او این روند را به خلاقیت عمل پیوند میزند؛ یک مفهوم مهم برای هگل.

