لودویگ ویتگنشتاین ترجمه مینا قاجارگر: این مقالۀ ویتگنشتاین در سال ۱۹۲۹ در جلد نهم سالنامۀ آریستوتلیَن سوسایتی ساپلیمنتری، که وابسته به جامعۀ ارسطوییان است، منتشر شد. ویتگنشتاین در این مقاله بر اهمیت توجه به جهان به جای تحلیل پیشینی زبان تاکید میکند. در نظر او، منطقی که ثمرۀ تحلیل پیشینی زبان است با واقعیت سازگار نیست و اجازۀ ساخت فرمهایی را میدهد که تنوع منطقی بیشتری نسبت به ساختار جهان واقعی دارند.
***
هر گزاره یک محتوا [ماده] و یک فرم [صورت] دارد. ما میتوانیم تصویر فرم محض را به دست آوریم اگر [آن را] از معنای واژههای مفرد یا نمادها (تا آنجایی که معانی مستقل دارند) انتزاع کنیم؛ یعنی، اگر به جای ثابتهای گزاره، متغیرهایی را جایگزین کنیم، [میتوانیم به صورت و فرم گزاره دست پیدا کنیم]. قوانین نحو که بر روی ثابتها اِعمال میشوند باید بر روی متغیرها نیز اِعمال شوند. منظور من از نحو در این معنای کلی کلمه، قوانینی است که به ما میگویند یک واژه در چه پیوندهایی [با واژههای دیگر] معنا میدهد و بدینترتیب ساختارهای بیمعنا را طرد میکنند. نحو زبان متعارف، آنچنان که مشهور است، برای این مقصود بسندگیِ کامل ندارد. نحو زبان متعارف در تمامی موارد از برساخت شبهگزارههای بیمعنا جلوگیری نمیکند (برساختهایی از قبیل «قرمز بلندتر از سبز است» یا «امر واقع، گرچه امری فینفسه است، باید قادر باشد که به امری برای خودم نیز تبدیل بشود» و ...).
اگر تلاش کنیم هر گزارۀ مفروضی را تحلیل کنیم، به طور کلی درمییابیم که آنها حاصل جمع، ضرب منطقی یا دیگر توابعِ صدقِ منطقیِ گزارههای سادهترند؛ اما اگر به اندازۀ کافی تحلیلمان را ادامه دهیم، باید به نقطهای برسیم که صورتهای گزارهای در آن، دیگر از ترکیب فرمهای گزارهایِ سادهتر تشکیل نشدهاند. باید در نهایت به پیوندِ نهاییِ عبارات برسیم، پیوندی بیواسطه که نمیتوان آن را بدون تخریبِ صورت گزارهای به معنای دقیق کلمه، تجزیه کرد. گزارههایی که این پیوند نهایی عبارات را بازمینمایند، به تبعیت از برتراند راسل، گزارههای اتمی مینامم. پس گزارههای اتمی هستههای هر گزارهای هستند، آنها حاویِ امر مادی هستند و کل امور باقیمانده تنها بسط این امر مادی است.
موضوع اصلیِ گزارهها را باید در آنها بجوییم. وظیفۀ نظریۀ شناخت یافتن گزارههای اتمی و فهم برساخت آنها از واژهها و نمادهاست. این وظیفه بسیار دشوار است و فلسفه تازه به سختی شروع به گلاویز شدن با آن کرده است. برای انجام این مهم چه روشی در اختیار داریم؟ یک نظر اینست که آنچه را که در زبان متعارف موجب بدفهمیهای بیپایان میشود در یک سمبولیسم مناسب بیان کنیم؛ یعنی، جاهایی که زبان متعارف ساختار منطقی را تغییر شکل میدهد، جایی که اجازۀ شکلگیریِ شبهگزاره ها را میدهد، جایی که یک عبارت را در بینهایت معنای مختلف استفاده میکند، باید آن را با سمبولیسمی جایگزین کنیم که تصویر واضحی ازساختار منطقی ارایه میدهد، شبهگزارهها را دفع میکند و عباراتِ آن را به نحو نامبهم به کار میگیرد. باری، تنها وقتی میتوانیم یک سمبولیسم واضح را جایگزین یک سمبولیسم نادقیق کنیم که پدیدههایی را که میخواهیم توصیف کنیم وارسی کنیم و سپس تلاش کنیم تا تنوع منطقیشان را بفهمیم؛ یعنی، تنها میتوانیم با چیزی که ممکن است آن را پژوهش منطقیِ خود پدیدهها نامید به تحلیل درست دست یابیم، یعنی، در یک معنای معین پژوهشِ پسینی و نه با گمانهزنی دربارۀ امکاناتِ پیشینی. اغلب وسوسه میشویم که از یک نظرگاه پیشینی بپرسیم: بالاخره، یگانه فرمهای گزارههای اتمی چه میتوانند باشند و بعد به عنوان پاسخ مثلاً بگوییم: گزارههای موضوعـمحمولی و اسنادی (رابطهای) با دو یا چند عبارت بیشتر، شاید، گزارههایی که محمولها و روابط را به یکدیگر مربوط میکنند و ...؛ اما به نظر من این صرفاً بازی با کلمات است.
صورتِ (فرم) اتمی را نمیتوان پیشبینی کرد؛ و تعجبآور میبود اگر پدیدههای واقعی چیز بیشتری برای آموختن به ما در مورد ساختارشان نمیداشتند. ما از طریق زبان متعارفمان که از صورتهای موضوعـمحمولی و اسنادی استفاده میکند، به سمت چنین حدسهایی درباره ساختار گزارههای اتمی، رهنمون میشویم؛ اما در این زمینه زبان ما گمراهکننده است: تلاش خواهم کرد تا با یک تشبیه این را توضیح دهم. دو صفحۀ موازی را در نظر بگیرید، صفحههای الف و ب. روی صفحۀ الف اشکالی ترسیم شده است، مثلاً بیضیها و مستطیلهایی در شکلها و اندازههای مختلف و وظیفۀ ما این است که تصاویر این اشکال را روی صفحۀ ب ایجاد کنیم. ما میتوانیم دو راه را از بین راههایی که برای انجام این کار وجود دارد تصور کنیم. میتوانیم ابتدا قانون بازتاب (افکنش) را اعمال کنیم- مثلاً بازتاب یا انعکاس متعامد یا هر نوع دیگر- و سپس شروع کنیم به منعکس کردن تمام اشکال از صفحۀ الف به صفحۀ ب بر طبق این قانون.
راه دوم اینست که اینگونه عمل کنیم: این قانون را وضع کنیم که هر بیضی در صفحۀ الف باید به صورت یک دایره روی صفحۀ ب پدیدار شود و هر مستطیل به صورت یک مربع. اگر به دلایلی ترجیح دهیم که روی صفحۀ ب فقط دایره و مربع باشد، این روش بازنمایی ممکن است برایمان مناسب باشد. البته از روی این تصاویر نمیتوان شکل دقیق تصاویر اصلی بر روی صفحۀ الف [بیضیها و مستطیلها] را فوراً استنباط کرد. تنها میتوانیم از طریق آنها نتیجه بگیریم که شکل اصلی بیضی یا مستطیل بوده است. اگر بخواهیم با یک نگاه پی ببریم که شکل اصلی مشخصاً چه بوده است، باید آن روش منحصر به فردی را که به عنوان مثال، یک بیضی بر طبق آن به یک دایره تبدیل شده است، بدانیم. مورد زبان متعارف کاملاً مشابه این مثال است.
اگر واقعیتِ بیضیها و مستطیلها در صفحۀ الف باشند، صورتهای موضوعـمحمولی و رابطهای با مربعها و دایرههای در صفحۀ ب متناظر است. این صورتها هنجارهای زبان خاص ماست که ما صورتهای منطقی مختلف بسیاری را به شیوههای مختلف بسیار بر روی آنها میافکنیم؛ و درست به همین دلیل نمیتوانیم از کاربرد این هنجارها بر صورت منطقیِ واقعی پدیدههای توصیف شده نتیجهای بگیریم- مگر نتایج بسیار مبهم. صورتهایی مثل «این مقاله خسته کننده است»، «هوا خوب است»، «من تنبلم» که هیچ نقطۀ اشتراکی با یکدیگر ندارند، به عنوان گزارههای موضوع-محمولی خودشان را عرضه میکنند، یعنی ظاهراً به مثابه گزارههایی با فرم یکسان.
حال اگر سعی کنیم به تحلیلی واقعی دست بیابیم، صورتهایی منطقی پیدا خواهیم کرد که شباهت بسیار کمی با هنجارهای زبان متعارف دارند. ما با تنوع کاملی از اشیای زمانمند و مکانمند مثل رنگها، صداها و غیره و غیره، با درجهبندیشان، تغییرهای مستمرشان و ترکیبهایشان در نسبتهای مختلف و تمام آن چیزهایی که نمیتوانیم با ابزارهای متعارف بیان به چنگشان آوریم، با صورتهای مکان و زمان روبرو میشویم. در اینجا میخواهم نخستین ملاحظۀ قطعی خودم را دربارۀ تحلیل منطقی پدیدههای واقعی اعلام میکنم: برای بازنمایی آنها [پدیدههای واقعی]، اعداد (گویا و اصم) باید وارد ساختار گزارههای اتمی شوند. من این مطلب را با مثالی توضیح میدهم.
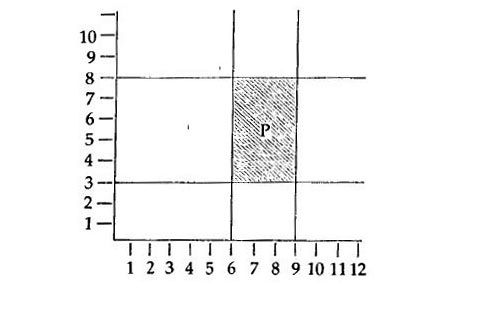
یک دستگاه مختصات را با محورهای عمود بر هم و مقیاس دلخواهِ ثابت در میدان دید خود تصور کنید. واضح است که ما میتوانیم شکل و موقعیت هر لکۀ رنگی را در میدان دید خود به وسیلۀ عبارات عددی که در نسبت با سیستم مختصات معنا دارند و یکایِ انتخاب شده توصیف کنیم؛ و همچنین واضح است که این توصیف تنوع منطقی درستی دارد و توصیفی که تنوع کمتری داشته باشد فایدهای نخواهد داشت. یک مثال ساده میتواند معرف لکۀ ج با عبارتِ [۸-۳ و ۹-۶] و گزارهای دربارۀ آن، مثلاً ج قرمز است، با نماد «[۸-۳ و ۹-۶] ق» باشد که در آن ق یک عبارتِ هنوز تحلیل نشده است («۸-۳» و «۹-۶» برای فاصلۀ پیوستۀ بین اعداد مربوطه وضع شدهاند).
دستگاه مختصات در اینجا بخشی از شیوۀ بیان است؛ بخشی از روش انعکاس که توسط آن واقعیت در سمبولیسم ما منعکس میشود. رابطۀ لکّهای که بین دو لکۀ دیگر قرار گرفته است به طور مشابه میتواند با استفاده از متغیرهای مشهود بیان شود. واضح است که این تحلیل به هیچوجه ادعای کامل بودن ندارد. من در آن هیچ اشارهای به زمان نکردهام و استفاده از فضای دو بعدی حتی در مورد دید یک طرفه نیز موجه نیست. فقط میخواهم به سمتی اشاره کنم که به عقیدۀ من، تحلیل پدیدههای بصری باید در آنسو جستجو شود و اینکه در این تحلیل ما با فرمهای منطقیای مواجهیم که کاملاً متفاوت از فرمهایی هستند که انتظار داریم در زبان متعارف با آنها مواجه شویم.
به عقیدۀ من، حضور اعداد در صورتهای گزارههای اتمی، صرفاً ویژگیِ یک سمبولیسم خاص نیست، بلکه یک ویژگی ذاتی و در نتیجه اجتنابناپذیر بازنمایی است؛ و اعداد- همانطور که در زبان متعارف هم میگوییم- باید زمانی که با ویژگیهایی که درجهبندی دارند سروکار داریم وارد این صورتها شوند؛ ویژگیهایی مثل طول یک بازه، زیر و بمیِ صدا، روشنی یا قرمزی یک سایۀ رنگ و ... . یکی از مشخصههای این ویژگیها اینست که یک درجه از آنها درجات دیگر را طرد و رفع میکند. یک سایۀ رنگ نمیتواند همزمان دو درجۀ مختلف از روشنی یا سرخی داشته باشد، یک صدا نمیتواند دو درجۀ متفاوت داشته باشد و... و نکتۀ مهم در اینجا اینست که این ملاحظات بیان کنندۀ یک تجربه نیستند بلکه به یک معنا توتولوژی هستند. هر یک از ما این نکته را در زندگی روزمره میدانیم. اگر کسی از ما بپرسد: «دمای بیرون چند است؟» و ما بگوییم «هشتاد درجه» و او دوباره بپرسد: «آیا نود درجه است؟» میگوییم: «به تو گفتم که هشتاد درجه است». ما گزارش دربارۀ درجه را (برای مثال درجۀ هوا) توصیف کاملی میدانیم که نیازی به تکمله ندارد؛ بنابراین وقتی کسی از ما میپرسد ساعت چند است، میگوییم ساعت چند است و نمیگوییم چند نیست.
ممکن است کسی فکر کند- و خود من تا چند وقت پیش اینگونه فکر میکردم- جملهای که درجۀ یک کیفیت را بیان میکند باید با فرآوردۀ منطقیِ گزارههایِ فردیِ کمی و یک گزارۀ مکملِ تکمیلی تحلیل شود. مثل اینکه من میتوانم محتوای جیب خود را با این گفته توصیف کنم که «در جیبم یک پنی، یک شیلینگ، دو کلید هست و چیز دیگری نیست». این «و چیز دیگری نیست» گزارهای تکمیلی است که توصیف را کامل میکند؛ اما این نوع تحلیل برای تحلیل یک گزاره در مورد درجه به کار نمیآید. به این دلیل که بیایید برای مثال واحد روشنایی را b بنامیم و (E(b جملهای باشد با این مضمون که شیء E این مقدار روشنایی دارد، در این صورت گزارۀ (E(2b که میگوید E دو درجه روشنایی دارد باید قابل تحلیل به فرآوردۀ منطقیِ (E(b)&E(b باشد، اما این جمله معادل (E(b است؛ از طرف دیگر اگر سعی کنیم بین واحدها تمایز قائل شویم و در نتیجه بنویسیم: (”E(2b)=E(b’)&E(b، در این صورت دو واحد مختلف روشنایی را فرض گرفتهایم و در نتیجه اگر یک شیء یک واحد روشنایی داشته باشد، این سؤال پیش میآید که کدام یک از این دو واحد؟’b یا ”b؟ که آشکارا مهمل است.
من گفتم گزارهای که یک درجه را به یک کیفیت نسبت میدهد، نمیتواند بیشتر تحلیل شود و به علاوه، اینکه رابطۀ اختلاف درجات، یک رابطۀ درونی است و بنابراین با یک رابطۀ درونی بین گزارههایی که درجات مختلف را نسبت میدهند بازنموده میشود. این یعنی، جملۀ اتمی باید همان تنوعی را داشته باشد که درجهای که نسبت میدهد داراست، پس در نتیجه اعداد باید وارد صورتهای گزارههای اتمی شوند. طرد متقابل گزارههایِ غیر قابلِ تحلیل دربارۀ درجات با نظری که من چند سال پیش منتشر کردم در تناقض است.آن نظر این بود که گزارههای اتمی نباید یکدیگر را طرد کنند. من اینجا تعمداً واژۀ «رفع» [طرد] را به کار میبرم و نه «تناقض» را، زیرا بین این دو مفهوم تفاوتی وجود دارد و گزارههای اتمی اگر چه نمیتوانند متناقض باشند، اما ممکن است همدیگر را رفع و طرد کنند. تلاش خواهم کرد که این را توضیح دهم.
توابعی وجود دارد که تنها در ازای یک مقدار برای آرگومانشان میتوانند گزارۀ صادق تحویل دهند، زیرا در آنها فقط جا برای یک مقدار هست. برای مثال گزارهای را در نظر بگیرید که وجود رنگ R در زمان معین T در مکان معین p در میدان دید ما را اعلام میکند. من این گزاره را به صورت “RPT” مینویسم و برای یک لحظه هر ملاحظهای در این باره که چگونه چنین جملهای باید بیشتر تحلیل شود را کنار میگذارم. بدین ترتیب، “BPT” میگوید که رنگ B در زمان T و مکان P قرار دارد و این برای اکثر ما در اینجا و برای همۀ ما در زندگی روزمره آشکار است که “BPT&RPT” یک نوع تناقض است (و نه صرفاً یک گزارۀ کاذب). اکنون اگر جملاتی که درجات را بیان میکنند تحلیلپذیر میبودند- آن طور که قبلاً فکر میکردم- میتوانستیم این تناقض را اینطور توضیح دهیم که رنگ R شامل تمام درجات R است و هیچ درجهای از B را در خود ندارد و همینطور رنگ B شامل تمام درجات B است و هیچ درجهای از R در خود ندارد؛ اما از سطور بالا نتیجه میشود که هیچ تحلیلی نمیتواند گزارههای مربوط به درجات را حذف کند. پس طرد متقابل RPT و BPT چگونه عمل میکند؟ به عقیدۀ من چنین چیزی مبتنی بر این واقعیت است که RPT همچون BPT به یک معنای معین کامل هستند. این امر در عالم واقع متناظر است با تابع ()PT که تنها برای یک موجود یک جای خالی دارد و در واقع تنها به یک رنگ اجازۀ ورود میدهد. مثل اینکه بگوییم روی صندلی فقط برای یک نفر جا هست. سمبولیسم ما که به ما اجازۀ ساخت فرآوردۀ منطقی “RPT”&”BPT”را میدهد، تصویر درستی از واقعیت را در اینجا به دست نمیدهد.
من در جای دیگری گفتهام که گزاره «به سوی واقعیت میرود» و منظورم این بود که صورتهای اشیاء، مشمول در صورت گزارهای هستند که در مورد این اشیا سخن میگوید؛ زیرا جمله به همراه روش انعکاس واقعیت در جمله، صورت منطقی اشیا را معلوم میکند، درست همانطور که در تشبیه ما، یک تصویر در صفحۀ ب، به همراه شیوۀ انعکاسش، شکل روی صغحۀ الف را معلوم میکند. این ملاحظه، به عقیدۀ من، کلیدی برای توضیح طرد متقابل RPT و BPT برای ما فراهم میکند؛ زیرا اگر گزاره شامل صورت آن موجودی باشد که در مورد آن سخن میگوید، آنگاه ممکن است که دو گزاره در همین صورت با یکدیگر تصادم پیدا کنند [و هم را دفع کنند]. گزارههای «براون الان روی این صندلی نشسته است» و «جونز الان روی این صندلی نشسته است»، هر کدام، به یک معنا، تلاش میکنند که موضوع خودشان را روی صندلی بنشانند؛ اما فرآوردۀ منطقی این دو گزاره، هر دو را بی درنگ روی صندلی مینشاند و این به یک تصادم خواهد انجامید، به طرد متقابل این عبارتها. این طرد چگونه خودش را در سمبولیسم نشان میدهد؟ ما میتوانیم فرآوردۀ منطقی [عطف منطقیِ] این دو گزاره، P و Q را به این طریق بنویسیم:
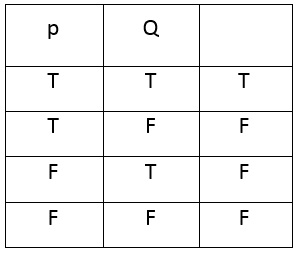
چه اتفاقی میافتد اگر این دو گزاره RPT و BPT باشند؟ در این مورد سطر اول T T T باید پاک شود چون یک ترکیب غیر ممکن را نشان میدهد. امکانهای صحیح در اینجا اینگونه است:
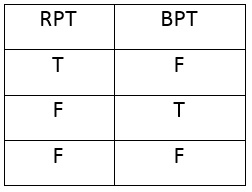
یعنی، فرآوردهای منطقی از این دو جمله، RPT و BPT، در معنای اول وجود ندارد و در اینجا مفهوم طرد مطرح است نه تناقض. تناقض اگر وجود داشته باشد، باید نوشته میشد
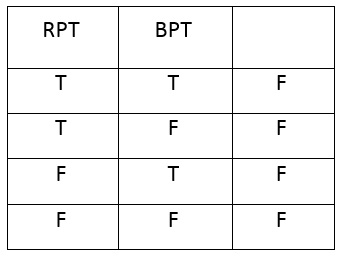
اما این بی معناست، زیرا سطر نخست، «T T F» به گزاره تنوع منطقی بیشتری در مقایسه با امکانات واقعی میدهد. البته این، نقص نمادسازی ماست که از شکلگیریِ چنین ساختارهای بی معنایی جلوگیری نمیکند و یک نمادسازی کامل باید چنین ساختارهایی را با قوانین خاص نحوی طرد کند و به آنها اجازۀ ساخته شدن ندهد. این قوانین باید به ما بگویند که ترکیبهای خاصی از صادقها و کاذبها در انواع خاصی از گزارههای اتمی که بر حسب ویژگیهای نمادینِ معینی توصیف شدهاند، باید کنار گذاشته شوند؛ اما چنین قوانینی ایجاد نمیشوند مگر اینکه عملاً به تحلیل نهایی پدیدههای مورد بحث دست یابیم؛ و چنان که همگی میدانیم، این امر هنوز برای ما حاصل نشده است.
این مقاله ترجمهای است از:
Wittgenstein, Ludwig. "Some remarks on logical form." Proceedings of the Aristotelian Society, Supplementary Volumes (1929): 162-171
منبع: ترجمان

